En este trabajo se
pretende mostrar cómo dentro de los problemas que se les plantean a los alumnos
en la educación primaria de México, subyacen cuestiones teóricas que el
profesor debe conocer para entender por qué fallan al responder las consignas
planteadas en los cuestionamientos.
Dentro de los temas
de este blog, se han publicado alguno referente a los problemas de tipo
aditivo. En esta ocasión buscando en los textos, se encuentra en el libro de
tercer grado de desafíos matemáticos, planteamientos que permiten analizar
ejercicios para resolverse empleando los pasos o estrategias que sugieren las
primeras tres categorías planteados por G. Vergnaud. Se muestran para entender
primero si el aspecto teórico mostrado es conocido o no por los docentes y
segundo para reflexionar entonces si el alumno ha practicado lo suficiente para
enfrentarse a este tipo de problemas, dicho de otro modo si conscientemente el
maestro ha trabajado gradualmente desde estrategias gráficas y posteriormente
actividades similares que sean resueltas con éxito y vayan encaminadas a el
empleo de operaciones o algoritmos cuando contesta una prueba, tarea o examen.
Para resolver este
tipo de planteamientos, el alumno debe comprender las consignas y reflexionar
sobre las preguntas particulares, en ningún momento se pretende convertir en
guía para resolver así las actividades. Es entendible que cada titular de grupo
conoce y aplica estrategias diferentes y llega a que sus alumnos contesten
correctamente este ejercicio.
En la primera
pregunta, (p. 91) imagen amarilla, se pide a los alumnos que contesten tres
preguntas, para ello se considera que primero debe de resolver la tercera
pregunta porque es la que nos indica dos datos, (cuántas canicas tenía Alberto
antes del juego y cuántas canicas después del juego)
Para la pregunta
dos, (cuadro azul) el planteamiento sugiere hacer una comparación (categoría 3), entonces si
el alumno está haciendo transformaciones, puede pensar que seguirá realizándolas.
Bueno esto es una suposición, el punto es que aparentemente los problemas son
similares y económicamente se resuelven ambos o con una suma o con una resta;
es cierto, pero en este planteamiento no hay un devenir sino una comparación,
más aun, una comparación de algo no tangible pero si medible como son años cumplidos.
En la imagen se presenta el esquema, gráficamente se puede comparar colocando
en un cuadro a un niño y no sé, tal vez
frente a ocho pastelitos o una línea del tiempo… como en las siguientes imágenes.
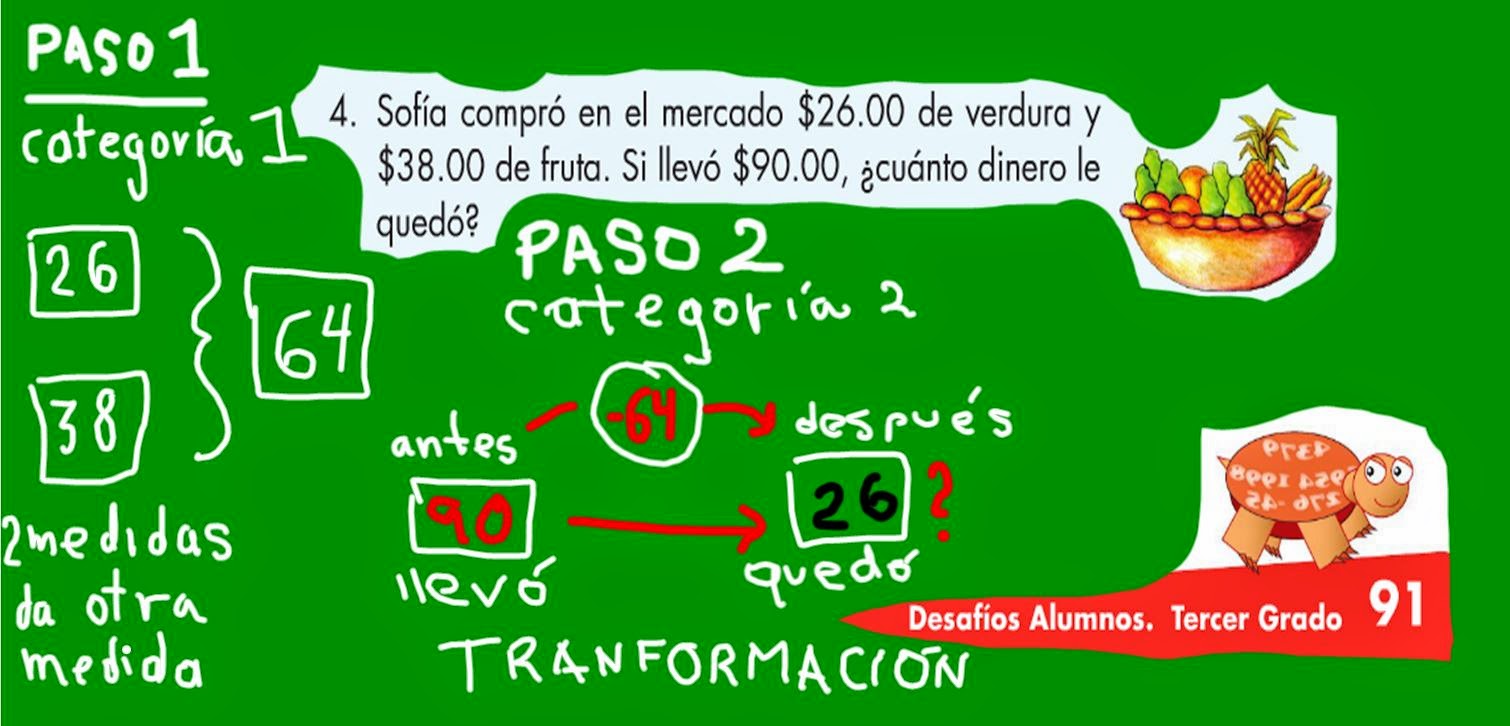
El último ejercicio de la página 91 (cuadro en verde), culmina con
un ejercicio donde se aprecia que se suman dos medidas para dar lugar a otra
medida… en los esquemas que han sido presentando, los números dentro de los cuadriláteros
representan medidas, no son ni positivos, ni negativos… mientras los escritos
en círculos son relativos, y éstos sí
son o positivos, o negativos. Bien la solución nos muestra, y el alumno debe
entender que esta sumando elementos que están en un mismo universo, en un todo…
aunque se tengan que distinguir sus partes: frutas + verduras igual a canasta
de alimentos. Este esquema de la primera categoría es el que comúnmente se
enseña en las aulas y con esa explicación se pretende que los niños resuelvan
planteamientos donde están presentes las otras categorías. (cfr. Chamorro; Vergnaud;
Nunes y Bryant).
La pregunta sin
embargo pide que se diga con cuánto dinero terminó la compra, entonces el
dinero que pago de los alimentos pasa de ser una medida a representar un número
relativo en el segundo paso ya que se requiere una transformación. Se inicia
con 90, el durante es el dinero gastado y la respuesta está en la segunda
medida… como se aprecia en la imagen anterior… qué lío para el niño, ¿verdad?
 Los
desafíos de sumas y restas continúan en la página 92, antes del ejercicio que
está en el cuadro rosa, está un crucigrama el cual omitimos en este análisis.
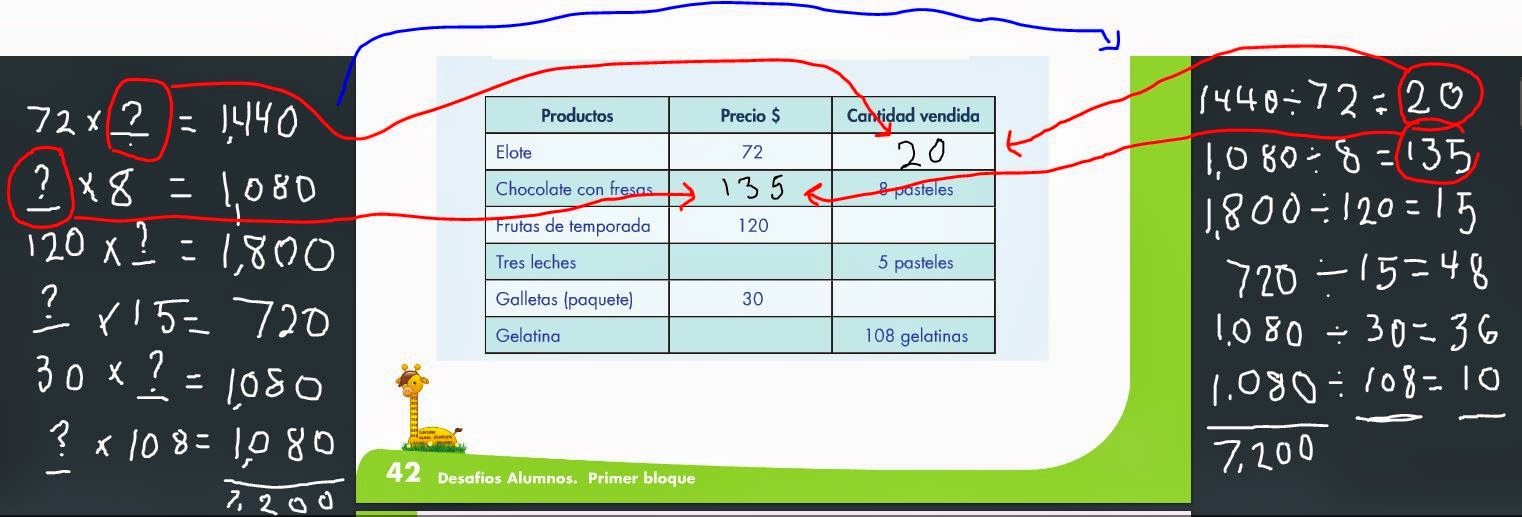
el ejercicio presentado al final de la página, es bastante interesante, se
sugiere resolverlo en tres pasos, es rico porque en el primero es una larga
transformación (categoría dos) en tres momentos; así encontramos respuesta a la
primera pregunta. La respuesta a la segunda pregunta es mediante la suma de dos
medidas (categoría uno). Y la respuesta a la tercera pregunta sugiere hacer una
comparación (categoría tres)
Los
desafíos de sumas y restas continúan en la página 92, antes del ejercicio que
está en el cuadro rosa, está un crucigrama el cual omitimos en este análisis.
el ejercicio presentado al final de la página, es bastante interesante, se
sugiere resolverlo en tres pasos, es rico porque en el primero es una larga
transformación (categoría dos) en tres momentos; así encontramos respuesta a la
primera pregunta. La respuesta a la segunda pregunta es mediante la suma de dos
medidas (categoría uno). Y la respuesta a la tercera pregunta sugiere hacer una
comparación (categoría tres)
Esta última imagen nos ayudaría a entender la comparación de manera gráfica.
Podemos entonces afirmar que es necesario entender los aspectos teóricos
dentro de la suma y resta (problemas aditivos) para poder apoyar a los niños
cuando se enfrentan a estos desafíos. Apoyarnos en imágenes, material concreto y
cualquier recurso que permita comprender al niño cuando une dos medidas... en qué momento
necesita hacer trasformaciones o si necesita hacer comparaciones para encontrar
la respuesta a los cuestionamientos.